Stochastic Neural Dynamics

Neural activity shows fluctuations and unpredictable transitions in its dynamics. This randomness can be an integral aspect of neuronal function; examples range from discrete fluctuations of ion channels to sudden sleep stage transitions involving the entire brain. To understand brain function as well as dysfunctions (i.e., brain pathologies), it is, therefore, necessary to develop modeling techniques and analysis of neuronal dynamics and data that explicitly incorporate such random components. Recent examples include the application of techniques derived from the theory of stochastic processes and statistical physics to the analysis and modeling of stochastic neuronal oscillations and progress in the analysis of stochastic neural network models.

Based on mathematical analysis, chiefly using nonlinear dynamical systems theory and probability theory, numerical simulations, and very recently, neurophysiological data analysis via machine learning techniques we can remark on the following research lines:

Dynamics of nonlinear localized waves (solitons) in neural networks

Nonlinear excitations of solitons type are localized solutions of a widespread class of weakly nonlinear dispersive partial differential equations. They originate from the balance between nonlinearity, dispersion, and or dissipation. In the neural systems, many theoretical studies have revealed the presence of such peculiar nonlinear waves. Many numerical studies report on the presence of deterministic nonlinear localized waves in a specific population of linked neurons under proper assumptions.

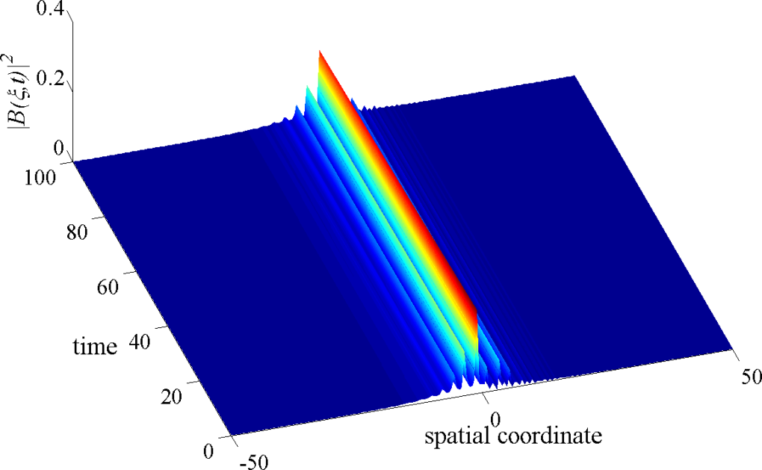
In our previous study, the first analytical form of the solitonic nerve impulse in a deterministic diffusively coupled Hindmarch-Rose (HR) neurons was established. To establish this analytic form, we use the Liénard form of the diffusive HR neuron model, we obtained a modified complex Ginzburg-Landau (CGL) equation which describes the evolution of modulated waves in this neural network, using a specific perturbation technique – the multiple-scale expansion in the semi-discrete approximation. We make use of the envelope soliton solution of the original CGL equation to obtain an analytic expression of the solitonic nerve impulse. The modulational instability in the diffusive HR neural network indicated the fact that due to the combine effects from nonlinearity, dispersion, and dissipation, a small perturbation on the envelope of a nerve impulse plane wave may induce an exponential growth of its amplitude, resulting in the carrier-wave breakup into a train of localized waves – solitions. From the biological point of view, this result suggests that neurons can participate in the collective processing of information, a relevant part of which is shared over all neurons but not concentrated at the single neuron level.

However, clear analytical solutions describing the dynamics of these diffusive nonlinear excitations in neural systems in the presence of stochasticity is completely lacking. The form and stability of the solitonic nerve impulse propagating in the neural network in the presence of randomness are very relevant because of the ubiquity of noise in neural systems and also because the form of the nerve impulse propagating in the neural system may stand as a signature to certain brain pathologies such as Migraines. The goal in this part of my research is to understand the role of noise in the emergence, propagation, and stability of the solitonic nerve impulse, and what consequences some noise limits might have on neural information processing.

Optimization of noise-induced resonance mechanisms in neural networks

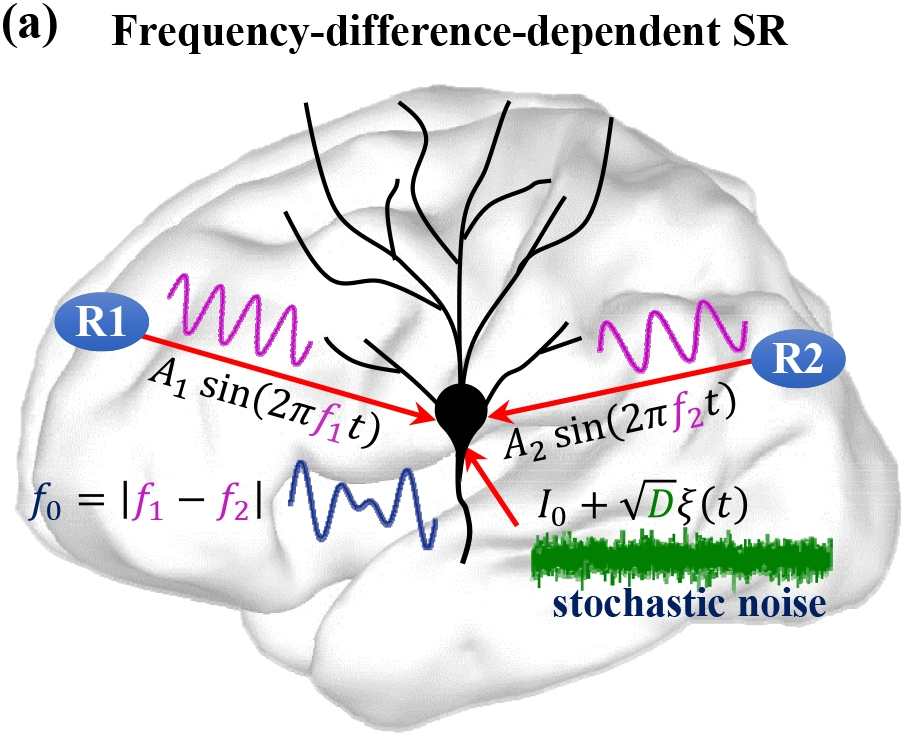
The functional role of noise has been a longstanding research question in neurobiology. While noise is generally undesired, its resonant effect is well known to be crucial to the proper functioning of neurons in terms of their information processing capabilities. There are several noise-induced mechanisms via which neurons optimize information processing, i.e., maximize the signal-to-noise ratio (SNR). These mechanisms include stochastic resonance (SR), coherence resonance (CR), self-induced stochastic resonance (SISR), inverse stochastic resonance (ISR), and recurrence resonance (RR).

The mathematical analysis of each of these stochastic mechanisms is well established in isolated neuron models, as well as in static neural networks. My previous work establishes the mathematical relations, within the framework stochastic slow-fast dynamical systems theory, between ISR and SISR, and also establishes the control scheme via which SISR controls CR in a multiplex neural network. However, more efficient optimization schemes for information processing that may emerge as a result of the interplay between one or more of these noise-induced resonance mechanisms and the dynamics of the neural network topology, have not yet been studied. These studies are still lacking.

Using the tools of geometric singular perturbation theory and multi-dimensional reaction rate theory with anisotropic diffusion, I am interested in two goals: (a) establishing the mathematical conditions required for the occurrence of SISR and CR in a biologically accurate -but high dimensional- neuron model; (b) developing optimization schemes based on the interactions of these noise-induced mechanisms in biologically relevant neural network topologies, which are themselves evolving according to specific learning rules.

References

Marius E. Yamakou, Poul G. Hjorth, Erik A. Martens. Optimal self-induced stochastic resonance in multiplex neural networks: electrical vs. chemical synapses. Frontiers in Computational Neuroscience 14, 62 (2020)
Marius E. Yamakou, Jürgen Jost. Control of coherence resonance by self-induced stochastic resonance in a multiplex neural network, Physical Review E 100, 022313 (2019)
Marius E. Yamakou, Jürgen Jost. Coherent neural oscillations induced by weak synaptic noise. Nonlinear Dynamics 93, 2121-2144 (2018)
Marius E. Yamakou, Jürgen Jost. Weak-noise-induced transitions with inhibition and modulation of neural oscillations. Biological Cybernetics 112, 445-463 (2018)
Marius E. Yamakou, Jürgen Jost. A simple parameter can switch between different weak-noise-induced phenomena in a simple neuron model. EPL (Europhysics Letters) 120, 18002 (2017)
F. M. Moukam Kakmeni, E. Maeva Inack, Marius E. Yamakou. Localized nonlinear excitations in diffusive Hindmarsh-Rose neural network. Physical Review E 89, 052919 (2014)