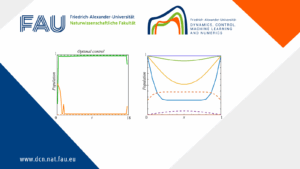
Control of a Lotka-Volterra System with Weak Competition
By Maicon Sônego Enrique Zuazua Introduction The Lotka-Volterra model reflects real ecological interactions where species compete for limited resources, potentially ...

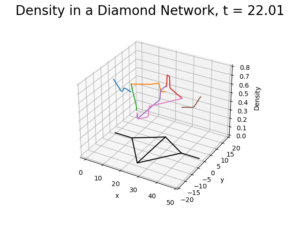
Mathematical modeling and numerical simulations for Gas Dynamics (on Networks)
Mathematical modeling and numerical simulations for Gas Dynamics (on Networks) By Sol G. Montero Carrasco Gas transport networks are essential ...
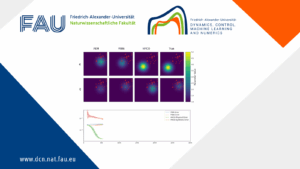
HYCO: The hybrid-collapse strategy for time-independent PDEs
HYCO: The hybrid-collapse strategy for time-independent PDEs By Matthys Jacobus Steynberg This post explores core ideas on a novel hybrid ...
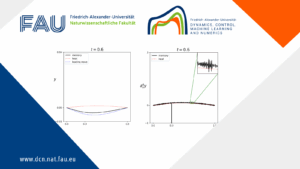
Hybrid parabolic-hyperbolic effect for heat equations with memory
Hybrid parabolic-hyperbolic effect for heat equations with memory By Yubiao Zhang 1 Introduction PDEs with memory involve the past values ...
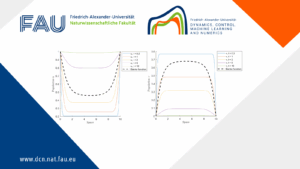
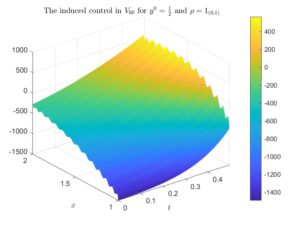
Boundary and Interior Control in a Diffusive Lotka-volterra Model
Boundary and Interior Control in a Diffusive Lotka-volterra Model By João Carlos Fernandes Barreira 1 Introduction 1.1 Problem formulation and ...
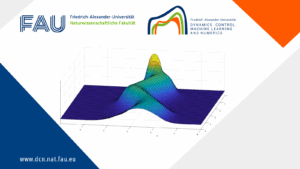
Optimal control of Fokker-Planck and transport equations using renormalized solutions
Optimal control of Fokker-Planck and transport equations using renormalized solutions By Christian Lange 1 Introduction The fundamental general optimal control ...

Mathematics & Philosophy: On the philosophical foundations of mathematics and its role as a structural science
Mathematics & Philosophy: On the philosophical foundations of mathematics and its role as a structural science By Christopher Sorg When ...
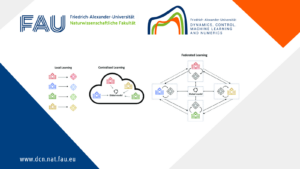
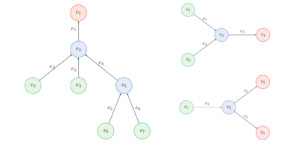
Federated Learning for Systems Identification
Federated Learning for Systems Identification By Noémie Turmel Federated learning (FL) operates in a decentralized manner, as shown Figure 1, ...

3−wave turbulence kinetics: Numerical approach for energy cascading
3−wave turbulence kinetics: Numerical approach for energy cascading By Arijit Das This post provides an overview of the results presented ...

How to steer a fleet of agents by controlling only a few: A mean-field approach
How to steer a fleet of agents by controlling only a few: a mean-field approach By Enrico Sartor 1 Introduction ...

Clustering in discrete-time self-attention
Clustering in discrete-time self-attention By Lucas Versini Since the article Attention Is All You Need [1] published in 2017, many ...

Low-rank balanced truncation of bilinear systems via Laguerre functions
Low-rank balanced truncation of bilinear systems via Laguerre functions By Zhihua Xiao Qiuyan Song, Yao-Lin Jiang, Zhen-Zhong Qi 1 Introduction ...
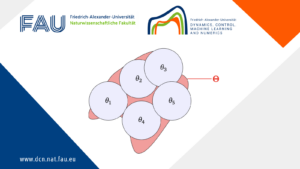
Generalization bounds for neural ODEs: A user-friendly guide
Generalization bounds for neural ODEs: A user-friendly guide By Lucas Versini Once a neural network is trained, how can one ...

Clustering in pure-attention hardmax transformers and its role in sentiment analysis
Clustering in pure-attention hardmax transformers and its role in sentiment analysis By Albert Alcalde This post provides an overview of ...

Partially dissipative hyperbolic systems without Fourier analysis
Partially dissipative hyperbolic systems without Fourier analysis By Ling-Yun Shou 1 Models We study the large-time behavior of the one-dimensional ...

A Turnpike Result for Optimal Boundary Control Problems with the Transport Equation under Uncertainty
A Turnpike Result for Optimal Boundary Control Problems with the Transport Equation under Uncertainty By Noboru Sakamoto Michael Schuster 1 ...
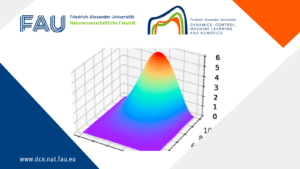
PINNs Introductory Code for the Heat Equation
PINNs Introductory Code for the Heat Equation By Ziqi Wang Martín Hernández Salinas This repository provides some basic insights on ...
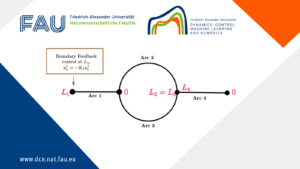
Limits of the stabilization of a networked hyperbolic system with a circle
Limits of the stabilization of a networked hyperbolic system with a circle By Martin Gugat Xu Huang 1 Introduction In ...

Stability of hyperbolic systems with non-symmetric partial dissipation
Stability of hyperbolic systems with non-symmetric partial dissipation By Timothée Crin-Barat Introduction In this post, we report new results for ...

Neural ODEs for interpolation and transport: From tight to shallow
Neural ODEs for interpolation and transport: From tight to shallow By Arselane Hadj Slimane, Internship. Master Student. ENS Paris-Saclay Introduction ...

Combined convection and diffusion in a network. A numerical analysis
Combined convection and diffusion in a network. A numerical analysis. By Dragoș Manea, Visiting PhD Student. Simion Stoilow Mathematical Institute ...

The ADMM-PINNs Algorithmic Framework for Nonsmooth PDE-Constrained Optimization: A Deep Learning Approach
The ADMM-PINNs Algorithmic Framework for Nonsmooth PDE-Constrained Optimization: A Deep Learning Approach By Yongcun Song, Postdoctoral Researcher at FAU DCN-AvH ...
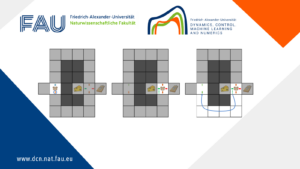
Reinforcement learning as a new perspective into controlling physical systems
Reinforcement learning as a new perspective into controlling physical systems By Theïlo Terrisse, Visiting PhD Student. L’Ecole des Ponts ParisTech ...
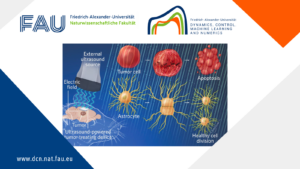
Null controllability for population dynamics with age, size structuring and diffusion
Null controllability for population dynamics with age, size structuring and diffusion By Yacouba Simpore, Visiting scientist from University of Fada ...

Breaking the symmetry with Robin boundary conditions
Breaking the symmetry with Robin boundary conditions By Alba Lia Masiello, Visiting PhD student from University of Naples Federico II ...

Convolutional autoencoders for very low-dimensional parametrizations of nonlinear fluid flow
Convolutional autoencoders for very low-dimensional parametrizations of nonlinear fluid flow By Jan Heiland, MPI for Dynamics of Complex Technical Systems ...
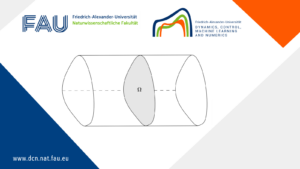
Torsional Rigidity: Classical and new results
Torsional Rigidity: Classical and new results By Gloria Paoli, Postdoctoral Researcher at FAU DCN-AvH Torsional rigidity is a key quantity ...

Federated Learning: Protect your data and privacy
Federated Learning: Protect your data and privacy By Ziqi Wang, PhD student at FAU DCN-AvH Code: A basic PyTorch implementation ...
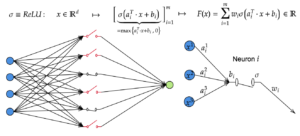
Breaking the curse of dimensionality with Barron spaces
Breaking the curse of dimensionality with Barron spaces By Antonio Álvarez López 1 Introduction Recent advances in computational hardware have ...

Stability results for the KdV equation with time-varying delay
Stability results for the KdV equation with time-varying delay By Hugo Parada Ríos Introduction The Korteweg-de Vries equation (KdV), is ...

Approximating the 1D wave equation using Physics Informed Neural Networks (PINNs)
Approximating the 1D wave equation using Physics Informed Neural Networks (PINNs) By Dania Sana Introduction Accurate and fast predictions of ...

Gas networks at stationary states: Analysis, software and visualization
Gas networks at stationary states: Analysis, software and visualization By Veronika Riedl Code: Files to run: nocircle.m, onecircle.m or twocircles.m ...
Sheep Herding Game
Author: Daniël Veldman, FAU DCN-AvH Code: A sheep herding game in MATLAB developed for the Long Night of Science #NdW22 ...

Lloyd’s Algorithm
Author: Martín Hernández, FAU DCN-AvH Code: In this repository, we show a code for Lloyd's algorithm. Also called Voronoid iteration, ...
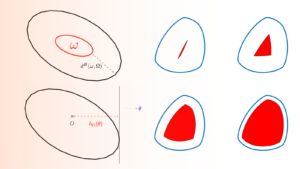
Using the support function for optimal shape design
Using the support function for optimal shape design By Ilias Ftouhi 1 Motivation Led by problems of optimal placement and ...
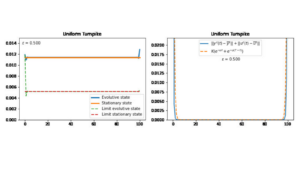
Uniform Turnpike Property
Uniform Turnpike Property By Martín Hernández Salinas 1 Introduction In this post, we analyze a 1 − d heat equation ...
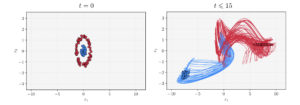
The interplay of control and deep learning
Author: Borjan Geshkovski, MIT The interplay of control and Deep Learning By Borjan Geshkovski It is superfluous to state the ...

Nonlinear hyperbolic systems: Modeling, controllability and applications
Nonlinear hyperbolic systems: Modeling, controllabiliy and applications By Yue Wang The control theory of hyperbolic systems is an important topic ...
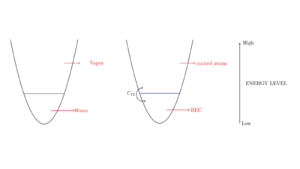
Kinetic theory of Bose Einstein Condensates
Kinetic theory of Bose Einstein Condensates By Minh-Binh Tran If a dilute gas of bosons, about one-hundred-thousandth the density of ...
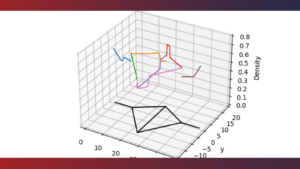
pyGasControls library (simulation software)
Author: Martin Gugat, Enrique Zuazua, Aleksey Sikstel, FAU DCN-AvH Code: [HINT] To run the software on your computer, you ...

Hamilton-Jacobi Equations: Inverse Design
Author: Carlos Esteve, Deusto CCM Code: In a previous post "Inverse Design For Hamilton-Jacobi Equations", described all the possible initial ...
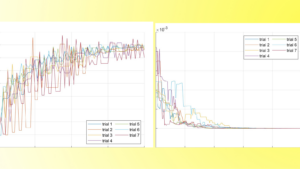
Random Batch Methods for Linear-Quadratic Optimal Control Problems
Author: Daniel Veldman, FAU DCN-AvH Code: || Also available @Daniël's GitHub In a previous post "Randomized time-splitting in linear-quadratic optimal ...
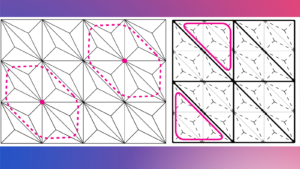
Augmented Lagragian preconditioners for incompressible flow
Author: Alexei Gazca, FAU DCN-AvH Code: Below is a description of the types of problems that can be tackled ...
Transition Layers in Elliptic Equations
Transition Layers in Elliptic Equations By Maicon Sônego Stable transition layers in an unbalanced bistable equation Consider the following semi-linear ...
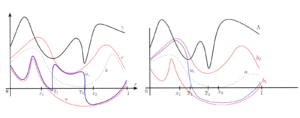
Randomized time-splitting in linear-quadratic optimal control
Randomized time-splitting in linear-quadratic optimal control By Daniël Veldman Introduction Solving an optimal control problem for a large-scale dynamical system ...

Felix Klein: A Legacy of Innovation in Mathematics and Education
Felix Klein: A Legacy of Innovation in Mathematics and Education By Roberto Rodríguez del Río, Complutense University of Madrid | ...
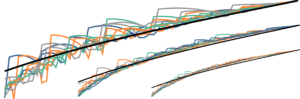
Control of Advection-Diffusion Equations on Networks and Singular Limits
Control of Advection-Diffusion Equations on Networks and Singular Limits By Jon Asier Bárcena-Petisco, Márcio Cavalcante, Giuseppe Maria Coclite, Nicola de ...

Probabilistic Constrained Optimization on Flow Networks
Probabilistic Constrained Optimization on Flow Networks Michael Schuster This research was funded by DFG in the SFB Transregio 154: Mathematical ...
Perceptrons, Neural Networks and Dynamical Systems
Perceptrons, Neural Networks and Dynamical Systems By Sergi Andreu // This post is last part of the "Deep Learning and ...

Deep Learning and Paradigms
Deep Learning and Paradigms By Sergi Andreu // This post is the 2nd. part of the "Opening the black box ...

Opening the black box of Deep Learning
Opening the black box of Deep Learning By Sergi Andreu Deep Learning is one of the three main paradigms of ...
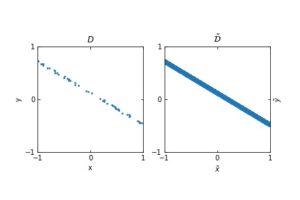
Averaged dynamics and control for heat equations with random diffusion
Averaged dynamics and control for heat equations with random diffusion By Jon Asier Bárcena Petisco, Enrique Zuazua Background and motivation ...
pyGasControls Framework
pyGasControls Framework By Martin Gugat, Enrique Zuazua, Aleksey Sikstel In order to optimize the operation of gas transportation networks, as ...
Model-based optimization of ripening processes with feedback modules
Model-based optimization of ripening processes with feedback modules By Michele Spinola 1 Important remark This contribution presents a proof of ...

Gas networks uncertainty and Probust constraints: model, distribution and optimization
Gas networks uncertainty and Probust constraints: model, distribution and optimization By Martin Gugat Gas transport and distribution systems are usually ...

Q-learning for finite-dimensional problems
Q-learning for finite-dimensional problems By Carlos Esteve Reinforcement Learning Reinforcement Learning (RL) is, together with Supervised Learning and Unsupervised Learning, ...

The interplay of control and deep learning
The interplay of control and Deep Learning By Borjan Geshkovski It is superfluous to state the impact deep (machine) learning ...

Neural networks and Machine Learning
Neural networks and Machine Learning By Marius Yamakou Neural Networks with time delayed connections Neurons communicate with each other through ...
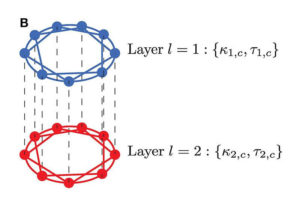
Stochastic Synchronization of Chaotic Neurons
Stochastic Synchronization of Chaotic Neurons By Marius Yamakou Real biological neurons can show chaotic dynamics when excited by the certain ...
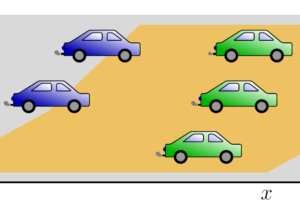
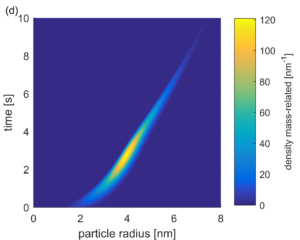
Nonlocal population balance equations and applications
Nonlocal population balance equations and applications By Michele Spinola Motivational example: look ahead behavior of car drivers When analyzing traffic ...
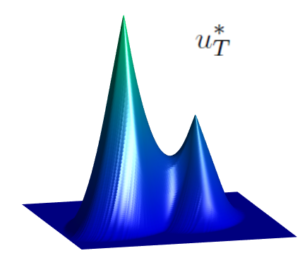
Inverse Design for Hamilton-Jacobi Equations
Inverse Design For Hamilton-Jacobi Equations By Carlos Esteve, Enrique Zuazua In many evolution models, the reconstruction of the initial state ...
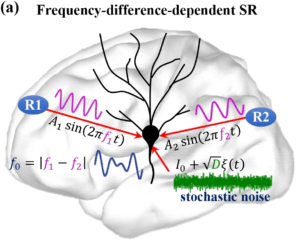
Stochastic Neural Dynamics
Stochastic Neural Dynamics By Marius Yamakou Neural activity shows fluctuations and unpredictable transitions in its dynamics. This randomness can be ...
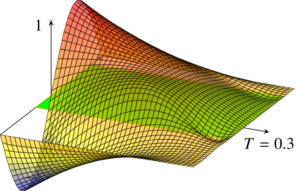
Controllability properties of fractional PDE
Controllability properties of fractional PDE By Umberto Biccari Controllability of the fractional heat equation Let \omega\subset (-1,1) be an open ...

Flows on Networks
Flows on Networks By Enrique Zuazua, Nicola de Nitti PDE models on Networks In the last few decades, models based ...

Stochastic optimization for simultaneous control
Stochastic optimization for simultaneous control By Umberto Biccari What is a simultaneous control problem? Consider the following parameter-dependent linear control ...

Convexity and Starshapedness of feasible sets in Stationary Flow Networks
Convexity and Starshapedness of feasible sets in Stationary Flow Networks By Martin Gugat Michael Schuster This research was funded by ...
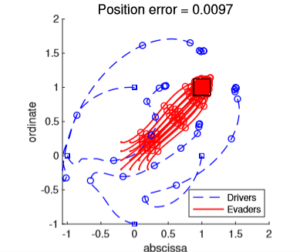
Collective dynamics modelling, Control and Simulation
Collective dynamics modelling, Control and Simulation By Dongnam Ko Collective dynamics Herds, packs, bird flocks, and fish schools are common ...

Data-Driven COVID Modeling
Classical models By Cyprien Neverov Compartmental epidemiological models [1] where introduced almost a century ago and are still considered the ...
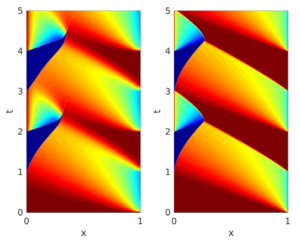
Non-local population balance equations
Non-local population balance equations By Michele Spinola Nichtlokale Populationsbilanzgleichungen. Der Verlauf des Weges wie zur Schule oder zur Arbeit hängt ...



